Question

It’s a snowy day and you’re pulling a friend along a level road on a sled. You’ve both been taking physics, so she asks what you think the coefficient of friction between the sled and the snow is. You’ve been walking at a steady 1.5 m/s, and the rope pulls up on the sled at a 30 ° angle. You estimate that the mass of the sled, with your friend on it, is 60 kg and that you’re pulling with a force of 75 N. What answer will you give?

Answer 1

`\mu_(k)=0.12`

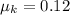
Step-by-step explanation:

In order to solve this problem we must first start by drawing a diagram of the situation. (See attached picture).

So we can start solving this problem by doing a sum of the forces in the y-direction so we get:

`\sum F_(y)=0`

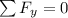
which yields:

`N+F_(y)-W=0`

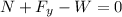
which can be solved for N so we get:

`N=W-F_(y)`

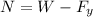
we know that:

`F_(y)=Fsin\theta`

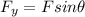
and that

W=mg

so we can substitute that into our original equation so we get:

`N=mg-Fsin\theta`

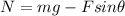
we can also substitute the provided data here so we get:

`N=(60kg)(9.81m/s^(2))-75Nsin(30^(o))`

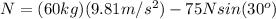
which yields:

N=551.1N

Next we can do a sum of forces in the x-direction so we get:

`\sum F_(x)=0`

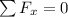
which gives us:

`F_(x)-f=0`

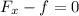
We know that the friction is given by the following formula:

`f=N\mu_(k)`

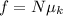
and that:

`F_(x)=Fcos \theta`

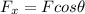
so we can substitute them into our sum of forces so we get:

`Fcos \theta - N\mu_(k)=0`

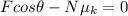
we can now solve this for
`\mu_(k)`:

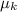which yields:

`\mu_(k)=(Fcos \theta)/(N)`

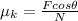
now we can substitute the provided data so we get:

`\mu_(k)=((75N)cos 30^(o))/(551.1N)=0.12`

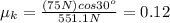
So the coefficient of kinetic friction between the sled and the snow is 0.12.