Question

Two satellites, one in geosynchronous orbit (T = 24 hrs) and one with a period of 12 hrs, are orbiting Earth. How many times larger than the radius of Earth is the distance between the orbits of the two satellites. (Mass(Earth) = 5.98 × 1024 kg, G = 6.67 × 10–11 N·m2, g = 9.81 m/s2, radius(Earth) = 6.38 × 106 m)

Answer 1

2.45 times

Step-by-step explanation:

In order to solve this problem, we must first start by drawing a diagram that will represent the situation (see attached picture).

Now if we analized the free body diagram we can see that the satellite is only affected by the force of gravity. This is the force that will cause the circular movement of the satellite. So if we did a sum of forces we would get:

`\sum F=ma_(c)`

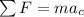
Since the only force exerted on the satellite is the force of gravity we den get:

`W=ma_(c)`

we know that the weight of the satellite is given by it's mass and acceleration of gravity so we get that:

`mg=ma_(c)`

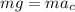
we can simplify it so we get:

`g=a_(c)`

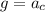
we know that centripetal acceleration is found by using the following formula:

`a_(c)=\omega^(2)r`

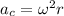
so

`g=\omega^(2)r`

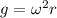
now, the universal gravity law gives us the following formula:

`F_(g)=G(mM)/(r^(2))`

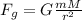
where m is the mass of the object, M is the mass of earth and r is the distance between the center of the earth and the object. We know that the force is equal to mg so we get:

`mg=G(mM)/(r^(2))`

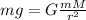
when simplifying we get:

`g=G(M)/(r^(2))`

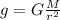
we can combine the previous equation with this one so we get:

`\omega^(2)r=G(M)/(r^(2))`

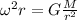
we can now solve this equation for r, so we get:

`r^(3)=G(M)/(\omega^(2))`

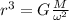
and

`r=\sqrt[3]{G(M)/(\omega^(2))}`

Regarding ω, we can find each of the angular speeds by doing some conversions:

`\omega_(1)=(1rev)/(24hr)*(1hr)/(3600s)*(2\pi rad)/(1 rev)=72.72x10^(-6)rad/s`

`\omega_(2)=(1rev)/(12hr)*(1hr)/(3600s)*(2\pi rad)/(1 rev)=145.44x10^(-6)rad/s`

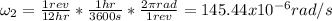
so we can substitute the data in the formula we got before:

`r=\sqrt[3]{G(M)/(\omega^(2))}`

`r_(1)=\sqrt[3]{(6.67x10^(-11)N(m^(2))/(kg^(2)))((5.98x10^(24)kg))/((72.72x10^(-6)rad/s)^(2))}`

`r_(1)=42.251x10^(6)m`

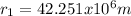
and

`r_(2)=\sqrt[3]{(6.67x10^(-11)N(m^(2))/(kg^(2)))((5.98x10^(24)kg))/((145.44x10^(-6)rad/s)^(2))}`

`r_(1)=26.62x10^(6)m`

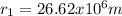
and now we can find the distance between the orbits of the two satellites:

`r_(1)-r_(2)=42.251x10^(6)m-26.62x10^(6)m=15.631x10^(6)m`

so:

`(15.631x10^(6)m)/(6.38x10^(6)m)=2.45`

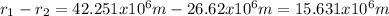
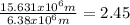
so the distance between the orbits of the two satellites is 2.45 times greater than the radius of the earth.