Question

Neon is compressed from 100 kPa and 24°C to 500 kPa in an isothermal compressor. Determine the change in the specific volume and specific enthalpy of neon caused by this compression. The gas constant of neon is R = 0.4119 kJ/kg·K, and the constant-pressure specific heat of neon is 1.0299 kJ/kg·K.

Answer 1

ΔV = -0.97 m³/ kg

ΔH = 0 kJ/ kg

Step-by-step explanation:

To determine the change in the specific volume we need to use the ideal gas law:

`PV = RT`

where P: pressure of the gas V: volume of the gas, R: ideal gas constant= 0.4119 kJ/kg.K = 0.4119 kPa.m³/kg.K and T: temperature of the gas.

The V₁, at a compressed pressure is:

`V_(1)= \frac {RT}{P_(1)}`

`V_(1)= \frac {0.4119 (kPa\cdot m^(3))/(kg\cdot K) \cdot (24 + 273 K)}{100 kPa}`

`V_(1)= 1.22 (m^(3))/(kg)`

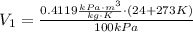
Similarly, the V₂ is:

`V_(2)= \frac {RT}{P_(2)}`

`V_(2)= \frac {0.4119 (kPa\cdot m^(3))/(kg\cdot K) \cdot (24 + 273 K)}{500 kPa}`

`V_(2)= 0.25 (m^(3))/(kg)`

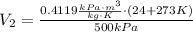
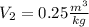
Now, the change in the specific volume because the compressor is:

`V_(2) - V_(1) = 0.25 - 1.22 (m^(3))/(kg)`

`V_(2) - V_(1) = -0.97 (m^(3))/(kg)`

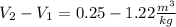
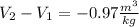
Finally, to calculate the change in the specific enthalpy, we need to remember that neon is an ideal gas and that is an isothermal process:

`\Delta H = C_(p) \cdot \Delta T`

`\Delta H = 1.0299 (kJ)/(kg \cdot K) \cdot 0`

`\Delta H = 0 (kJ)/(kg)`

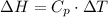
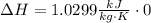
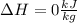
Have a nice day!