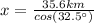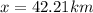Answer: 42.21 km
Explanation:
We can solve this using trigonometry, since we have the following data:
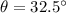 is the the angle of elevation
is the the angle of elevation
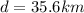 is the horizontal distance between the plane and the radar station
is the horizontal distance between the plane and the radar station
 is the hypotenuse of the right triangle formed between the radar station and the airplane
is the hypotenuse of the right triangle formed between the radar station and the airplane
Now, the trigonometric function that will be used is cosine:
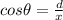 because
because
 is the adjacent side of the right triangle
is the adjacent side of the right triangle
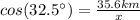
Finding
 :
: