Step-by-step explanation:
Given that,
Mass of the person, m = 72.5 kg
Initial speed of the car, u = 20.5 m/s
(a) Let
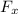 is the horizontal component of the average force, in newtons, on the person if he is stopped by a padded dashboard that compresses an average of 1.15 cm, x = 0.0115 m and v = 0
is the horizontal component of the average force, in newtons, on the person if he is stopped by a padded dashboard that compresses an average of 1.15 cm, x = 0.0115 m and v = 0
Using the second law of motion to find it as:
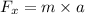
Using the third equation of kinematics to find a.
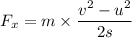
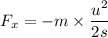
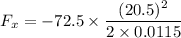
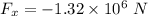
(b) Here, x = 13.5 cm = 0.135 m
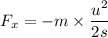
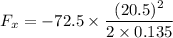

Hence, this is the required solution.