Answer:
D. ∠B = ∠B' = 74° and ∠C = ∠C' = 66°
Explanation:
Given,

We know,sum of all 3 angles of a triangle is
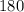 °
°
Doing so ,

Simplifying all like terms,
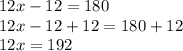
Dividing both side by 12
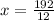
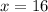
Now we plug this in each angles and find their exact values.
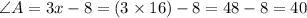 °
°
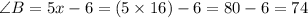 °
°
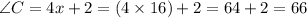 °
°
Now substituting the
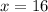 in angles of dilated triangle.
in angles of dilated triangle.
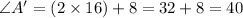 °
°
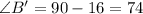 °
°
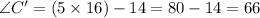 °
°
We see that all the corresponding angles are equal and as far as the options are concerned only option (D) matches.