Answer:
(5, -2)
Explanation:
The equation of the ellipse is given by:
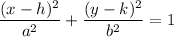
where
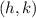 is the center of the ellipse.
is the center of the ellipse.
The given equation of the ellipse is:
x² + 2y² - 10x + 8y + 25 = 0.
We have to reduce to the standard form so that we can compare and determine the center of the ellipse.
Subtracting
 from the equation on both sides, we get:
from the equation on both sides, we get:
x² - 10x + 2y² + 8y + 25 - 25 = - 25


The next step would be complete the squares. Let us complete
 first.
first.
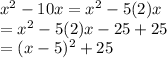
Now for
 .
.
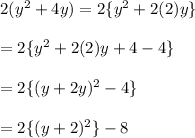
Therefore the equation becomes:
(x - 5)² + 2(y + 2)² = -25 + 25 + 8
⇒ (x - 5)² + 2(y - 2)² = 8
Since the
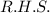 needs 1, we divide the entire equation by 8.
needs 1, we divide the entire equation by 8.
⇒
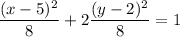
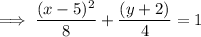
Comparing with standard form we get:
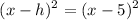 and
and
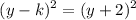
⇒ (h,k) = (5,-2)
∴ The center of the ellipse is (5,-2).