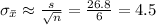Question

A teacher was interested in knowing the amount of physical activity that his students were engaged in daily. He randomly sampled six students in his class and recorded the number of minutes that they exercised in the past day. The numbers were 30mins, 40 mins, 60 mins, 80 mins, 20 mins, and 85 mins. What’s the standard error of the mean

Answer 1

4.5

Explanation:

Answer 2

The standard error of the mean is 4.5.

Explanation:

As we don't know the standard deviation of the population, we can estimate the standard error of the mean from the standard deviation of the sample as:

`\sigma_{\bar{x}}\approx(s)/(√(n))`

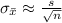
The sample is [30mins, 40 mins, 60 mins, 80 mins, 20 mins, 85 mins]. The size of the sample is n=6.

The mean of the sample is:

`\bar{x}=\frac{1}n} \sum x_i =(30+40+60+80+20+85)/(6)=52.5`

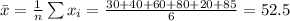
The standard deviation of the sample is calculated as:

`s=\sqrt{(1)/(n-1)\sum (x_i-\bar x)^2} \\\\ s=\sqrt{(1)/(5)\cdot ((30-52.5)^2+(40-52.5)^2+(60-52.5)^2+(80-52.5)^2+(20-52.5)^2+(85-52.5)^2}\\\\s=\sqrt{(1)/(5) *3587.5}=√(717.5)=26.8`

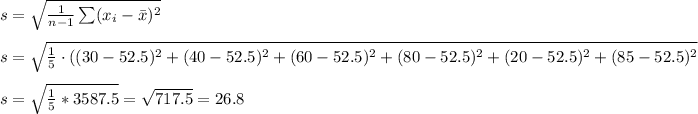
Then, we can calculate the standard error of the mean as:

`\sigma_{\bar{x}}\approx(s)/(√(n))=(26.8)/(6)= 4.5`