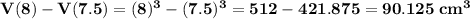Question

The edge of a cube was measured to be 8 cm, with a maximum possible error of 0.5 cm. Use a differential to estimate the maximum possible error in computing the volume of the cube. (This next part is ungraded, just for fun. Using a calculator, find the actual error in measuring volume if the radius was really 8.5 cm instead of 8 cm, and find the actual error if the radius was actually 7.5 cm instead of 8 cm. Compare these errors to the answer you got using differentials).

Answer 1

96 cc

102.125 cc

90.125 cc

Explanation:

Let V(x) the volume of a cube of edge x cm. Then

`\bf V(x)=x^3 \;cm^3`

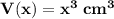
The maximum possible error in computing the volume of the cube would be

V(8+0.5) - V(8)

By approximating with the derivative, we know

V(8+0.5) ≅ V(8) +0.5V'(8)

hence

V(8+0.5) - V(8) ≅ 0.5V'(8)

But

`\bf V'(x)=3x^2\Rightarrow V'(8)=3*64=192`

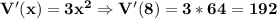
and maximum possible error in computing the volume of the cube would be approximately 0.5*192 = 96 cc.

find the actual error in measuring volume if the radius was really 8.5 cm instead of 8 cm

`\bf V(8.5) - V(8) = (8.5)^3-8^3=614.125-512=102.125\;cm^3`

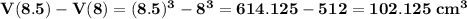
find the actual error if the radius was actually 7.5 cm instead of 8 cm.

`\bf V(8) - V(7.5) = (8)^3-(7.5)^3=512-421.875=90.125\;cm^3`