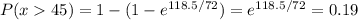Question

he time between telephone calls to a cable television service call center follows an exponential distribution with a mean of 1.2 minutes. a. What is the probability that the time between the next two calls will be 45 seconds or​ less? b. What is the probability that the time between the next two calls will be greater than 118.5 ​seconds?

Answer 1

a. The probability that the time between the next two calls will be 45 seconds or​ less is 46%.

b. The probability that the time between the next two calls will be greater than 118.5 seconds is 19%.

Explanation:

The cumulative density function of the exponential distribution for x≥0 is:

`F(x;\lambda)=1-e^(-\lambda x)`

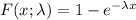
In this case,

`\lambda=1/\mu=1/1.2 \,min^(-1)=(1)/(1.2) *(1)/(min)*(1\,min)/(60s)=  (1)/(72) \, s^(-1)`

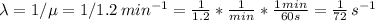
a) What is the probability that the time between the next two calls will be 45 seconds or​ less?

The probability that the time between the next two calls will be 45 seconds or​ less is 46%.

`P(x\leq45)=1-e^(45/72)=1-0.54=0.46`

b) What is the probability that the time between the next two calls will be greater than 118.5 ​seconds?

The probability that the time between the next two calls will be 118.5 seconds or​ less is 19%.

`P(x>45)=1-(1-e^(118.5/72))=e^(118.5/72)=0.19`