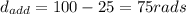Answer:
a).
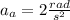
b).
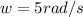
c).
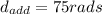
Step-by-step explanation:
Using the equations for angular motion
a).
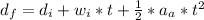
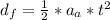
The initial position is zero as well as the initial speed so to know the angular accelerations replacing numeric
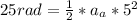
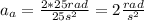
b).
The angular velocity can find knowing the distance it rotates for the time so far so:
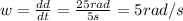
c).
The additional angle will the disk turn during the next 5.0s is
Total time 10s however we want to know the additional so the difference os the distance in the total and the distance already have is the additional angle so:
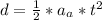
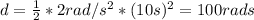
So: