Question

In an article in Marketing Science, Silk and Berndt investigate the output of advertising agencies. They describe ad agency output by finding the shares of dollar billing volume coming from various media categories such as network television, spot television, newspapers, radio, and so forth.Suppose that a random sample of 392 U.S. advertising agencies gives an average percentage share of billing volume from network television equal to 7.41 percent, and assume that alpha equals 1.43 percent. Calculate a 95 percent confidence interval for the mean percentage share of billing volume from network television for the population of all U.S. advertising agencies.

Answer 1

Answer: (7.27%, 7.55%)

Explanation:

As per given , we have

Sample size : n= 392

Sample mean :
`\overline{x}=7.41\%`

`\sigma=1.43\%`

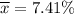
Critical two-tailed z-value for 95% confidence =
`z_(\alpha/2)=1.96`

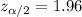
Required confidence interval would be :

`7.41\%\pm (1.96)(1.43\%)/(√(392))\\\\=7.41\%\pm 0.14\%\\\\=(7.27\%, 7.55\%)`

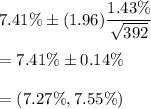
Hence, the required 95% confidence interval for the mean percentage share of billing volume from network television for the population of all U.S. advertising agencies : (7.27%, 7.55%)