Answer:
g/f = {(-1, 2)}
domain of g/f = {-1}
Explanation:
Given,
f = {(-1, 4),(1, 9),(4, 0)},
g = {(-1, -8),(2, -7),(4, 8),(5, -9)}
So, Domain of f = {-1, 1, 4},
Domain of g = {-1, 2, 4, 5}
Since,
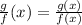
Thus, domain of g/f = Domain of f ∩ Domain of g = {-1, 4}
If x = -1,
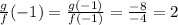
If x = 4,
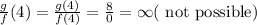
Hence, the domain of g/f = {-1}
And, g/f = {(-1, 2)}