Question

Suppose that the number of drivers who travel between a particular origin and destination during a designated time period has a Poisson distribution with parameter μ = 20 (suggested in the article "Dynamic Ride Sharing: Theory and Practice"†). (Round your answer to three decimal places.) (a) What is the probability that the number of drivers will be at most 18?

Answer 1

0.381 is the probability that the number of drivers will be at most 18.

Explanation:

We are given the following information in the question:

The number of drivers who travel between a particular origin and destination during a designated time period has a Poisson distribution with parameter μ = 20.

• The Poisson distribution is the discrete probability distribution of the number of events occurring in a given time period, given the average number of times the event occurs over that time period.
• The variance of Poisson distribution is equal to the mean of Poisson distribution.

a) P(number of drivers will be at most 18)

Formula:

`P(X =k) = \displaystyle(\mu^k e^(-\mu))/(k!)\\\\ \mu \text{ is the mean of the distribution}`

`P( x \leq 18) =P(x=0) + P(x =1) + P(x = 2) + ... + P(x = 18)\\\\= \displaystyle(20^0 e^(-20))/(0!) + \displaystyle(20^1 e^(-20))/(1!) +...+ \displaystyle(20^(18) e^(-20))/(18!)\\\\ = 0.381`

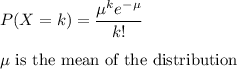
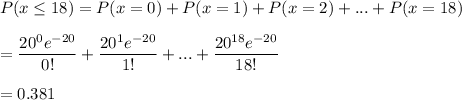
Thus, 0.381 is the probability that the number of drivers will be at most 18.