Question

Suppose that 1 month before the election a random sample of 500 registered voters are surveyed. From this sample 270 indicate that they plan to vote for Smith. Based on this survey data, find the 95% confidence interval estimate of Smith’s current support.

Answer 1

[ 0.4964, 0.5836 ]

Explanation:

Data provided in the question:

Total sample size = 500

person voting for smith = 270

thus,

P( person voting for smith ), p =
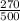`(270)/(500)` = 0.54

Confidence level = 95%

now,

standard error, SE =
`\sqrt{(p(1-p))/(n)`

or

SE =
`\sqrt{(0.54(1-0.54))/(500)`

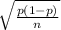
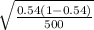
or

SE = 0.0223

now,

Confidence interval = p ± ( z × SE )

here,

z value for 95% confidence interval is 1.96

Confidence interval = [ 0.54 - ( 1.96 × 0.0223 ), 0.54 + ( 1.96 × 0.0223 ) ]

= [ 0.54 - 0.0436 , 0.54 + 0.0436 ]

= [ 0.4964, 0.5836 ]