Required answer:
- 0
- Not Defined
Detailed explanation:
To find the slope of the line, given that it passes through two points, use the formula:
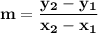
Where:
Plug in the data:
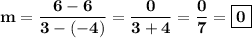
- - - - - - - - - - - - - - - - - - - - - -
Given the pair of points: (-5,8) and (-5,-6), plug them into the slope formula:
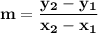
Evaluate:
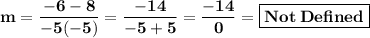
- - - - - - - - - - - - - - - - - - - - - - -