Answer:
The radius is growing at the rate of 0.09 centimeter per second at the instant it pops.
Explanation:
We are given the following information in the question:
A spherical balloon is designed to pop at the instant its radius has reached 3 centimeters.
The balloon is filled with helium at a rate of 10 cubic centimeters per second .
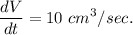
We have to find fast the radius is growing at the instant it pops.
Volume of spherical balloons =
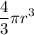
Differentiating, we get,
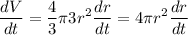
Putting the values, we get,

The radius is growing at the rate of 0.09 centimeter per second at the instant it pops.