Question

Part l:find the x-intercepts of the parabola and write them as ordered pairs. Hint: the x-intercepts are the points at which the function crosses the x-axis and y=0. Show your work

Part ll:Write the equation y=(x-4)(x+2) in standard form. Show your work.
Part lll:with the standard form of the equation from part ll, use the quadratic formula to identify the x-value of the vertex. Hint: the x-value of the vertex is -b/2a. Show your work
Part lV:substitute the x-value of the vertex from part lll into the original equation to find the y-value of the vertex. Then, write the coordinates of the vertex

Answer 1

Part 1) The x-intercepts are the points (-2,0) and (4,0)

Part 2)
`y=x^(2) -2x-8`

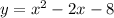
Part 3) The x-coordinate of the vertex is 1

Part 4) The y-coordinate of the vertex is -9 and the coordinate of the vertex is the point (1,-9)

Explanation:

we have

`y=(x-4)(x+2)`

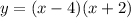
Part 1) Find the x-intercepts of the parabola and write them as ordered pairs

The x-intercepts are the values of x when the value of y is equal to zero

so

For y=0

`(x-4)(x+2)=0`

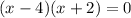
For x=4 and x=-2 the equation is equal to zero

therefore

The x-intercepts are the points (-2,0) and (4,0)

Part 2) Write the equation y=(x-4)(x+2) in standard form

The quadratic equation in standard form is equal to

`y=ax^(2) +bx+c`

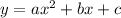
applying distributive property

`y=(x-4)(x+2)\\\\y=x^(2)+2x-4x-8\\\\ y=x^(2) -2x-8`

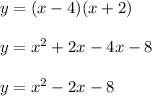
where

`a=1, b=-2,c=-8`

Part 3) With the standard form of the equation from part ll, use the quadratic formula to identify the x-value of the vertex

we know that

the x-value of the vertex is -b/2a

we have

`a=1, b=-2,c=-8`

substitute

`-(b)/(2a)=-((-2))/(2(1))=1`

therefore

The x-coordinate of the vertex is 1

Part 4) Substitute the x-value of the vertex from part lll into the original equation to find the y-value of the vertex.

we have

`y=(x-4)(x+2)`

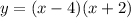
For x=1

substitute and solve for y

`y=(1-4)(1+2)`

`y=(-3)(3)`

`y=-9`

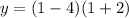
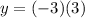
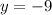
therefore

The y-coordinate of the vertex is -9

The coordinate of the vertex is the point (1,-9)