Answer:
The below graph with portion enclosed by red lines is the solution to the given equations.
Explanation:
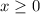 means the portion to the right of
means the portion to the right of
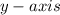
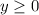 means the portion up of the
means the portion up of the
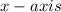
For
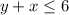 , we find
, we find
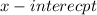 and
and
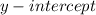
For
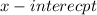 we substitute y=0
we substitute y=0
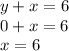 ,thus pont is
,thus pont is
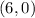
Similary
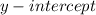 , we substitute x=0
, we substitute x=0
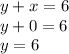 , thus point is
, thus point is
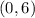
We connect these these two points and consider the below area as it contains less than inequality
For
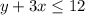 we again find the
we again find the
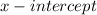 and
and
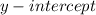
For
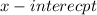 we substitute y=0
we substitute y=0
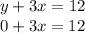
divide both side by
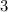 , we get
, we get
 , thus point is
, thus point is
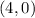
Similary
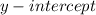 , we substitute x=0
, we substitute x=0
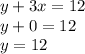
Thus point is
 ,
,
Now connect these two points and consider the area below the line as it contains less than inequality.
Finally the area enclosed by all these lines is the solution to the given equations, that is shown below.