Question

The inverse demand for a drug that treats melanoma is given by P = 3,000 – 10Q, where Q measures the number of drug treatments and P is the price per treatment. Suppose that the marginal cost per drug treatment is constant at $10. What is the profit-maximizing price per drug treatment?

Answer 1

Profit-maximizing price per drug treatment is $2,000

Step-by-step explanation:

The "cost of production" (cost of providing all treatments) is given by the area under the cost curve

(The cost curve is the straight line C = 10Q)

It is a right triangle with one side being the quantity (Q) and the other being the cost of the last unit being produced (10Q)

So the cost of production is:
`5Q^(2)`

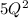
Revenue is given by P * Q = (3,000 - 10Q) * Q

Profit = Revenue - Cost of production = 3,000Q -
`10Q^(2)` -
`5Q^(2)`

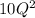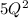
To find maximum, take derivative and solve for:

3,000 - 30Q = 0 => Q = 100

Profit-maximizing quantity is 100. The price will then be P = 3,000 - 10*100 = $2,000