Answer:
Option d that is graph D is the final answer.
Explanation:
We know that
 is an odd function.
is an odd function.
As odd functions are:
-
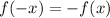
- Symmetric about opposite quadrant.
For
 we have the graph on Ist and IIIrd quadrant.
we have the graph on Ist and IIIrd quadrant.
And for
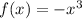 the graph will be on IInd and IVth quadrant.
the graph will be on IInd and IVth quadrant.
So if the leading term that is
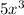 becomes
becomes
 (negative) the graph will be plotted on IInd and IVth quadrant.
(negative) the graph will be plotted on IInd and IVth quadrant.
There is also a constant terms
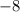 which means that it will intersect the
which means that it will intersect the
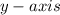 below the origin at
below the origin at
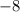 .
.
So from the above we can conclude that graph D is the answer.