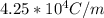Question

Assume this 1.20-mm-radius copper wire is electrically neutral in the Earth reference frame, in which it is at rest and carrying a current. Calculate the linear charge density λ′ of the copper wire in a reference frame moving along with the electrons if the electrons are moving at 5.20 ×10−4m/s .

Answer 1

The charge density in the system is
`4.25*10^4C/m`

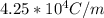
Step-by-step explanation:

To solve this problem it is necessary to keep in mind the concepts related to current and voltage through the density of electrons in a given area, considering their respective charge.

Our data given correspond to:

`r=1*10^(-3)m\\v = 5.2*10^(-4)m/s\\e= 1.6*10^(-19)C`

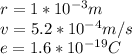
We need to asume here the number of free electrons in a copper conductor, at which is generally of
`8.5 *10^(28)m^(-3)`

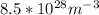
The equation to find the current is

`I = VenA`

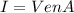
Where

I =Current

V=Velocity

A = Cross-Section Area

e= Charge for a electron

n= Number of free electrons

Then replacing,

`I = (5.2*10^(-4))(1.6*10^(-19))(88.5 *10^(28))(\pi(1*10^(-3))^2)`

`I= 22.11a`

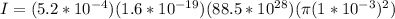
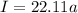
Now to find the linear charge density, we know that

`I = (Q)/(t) \rightarrow Q = It`

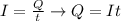
Where:

I: current intensity

Q: total electric charges

t: time in which electrical charges circulate through the conductor

And also that the velocity is given in proportion with length and time,

`V_d = (l)/(t) \rightarrow l = V_d t`

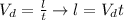
The charge density is defined as

`\lambda = (Q)/(l)\\\lambda = (It)/(V_d t)\\\lambda = (I)/(V_d)`

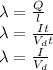
Replacing our values

`\lambda = \frac{22.11}{5.20*10{-4}}`

`\lambda= 4.25*10^4C/m`

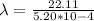
Therefore the charge density in the system is
`4.25*10^4C/m`