Answer:
a) The number of passengers that will maximize the revenue received from the flight is 99.
b) The maximum revenue is $48,609.
Explanation:
We have to analyse two cases to build a piecewise function.
If there are 80 or less passengers, we have that:
The cost of the trip is $586 for each passenger. So
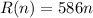
If there are more than 80 passengers.
There is a refund of $5 per passenger for each passenger in excess of 80. So the cost for each passenger is
 .
.
So we have the following piecewise function:
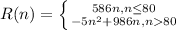
The maxium value of a quadratic function in the format of
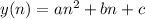 happens at:
happens at:
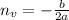
The maximum value is:
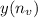
So:
(a) Find the number of passengers that will maximize the revenue received from the flight.
We have to see if
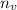 is higher than 80.
is higher than 80.
We have that, for
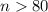 ,
,
 , so
, so
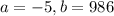
The number of passengers that will maximize the revenue received from the flight is:

Rounding up, the number of passengers that will maximize the revenue received from the flight is 99.
(b) Find the maximum revenue.
This is
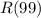 .
.


The maximum revenue is $48,609.