Question

Triangle S R Q is shown. Angle S R Q is a right angle. An altitude is drawn from point R to point T on side S Q to form a right angle. The length of S T is 9 and the length of T Q is 16. The length of S R is x. What is the value of x? 12 units 15 units 20 units 24 units

Answer 1

b

Explanation:

Answer 2

Option B.

Explanation:

It is given that ΔSRQ is a right angle triangle, ∠SRQ is right angle.

RT is altitude on side SQ, ST=9, TQ=16 and SR=x.

In ΔSRQ and ΔSTR,

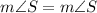`m\angle S=m\angle S` (Reflexive property)

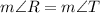`m\angle R=m\angle T` (Right angle)

By AA property of similarity,

`\triangle SRQ\sim \triangle STR`

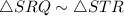
Corresponding parts of similar triangles are proportional.

`(SR)/(SQ)=(ST)/(SR)`

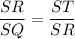
Substitute the given values.

`(x)/(9+16)=(9)/(x)`

`(x)/(25)=(9)/(x)`

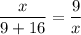
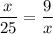
On cross multiplication we get

`x^2=25* 9`

`x^2=225`

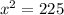
Taking square root on both sides.

`x=√(225)`

`x=15`

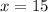
The value of x is 15. Therefore, the correct option is B.