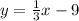Question

What is the equation of this graphed line?

A graph with a line running through coordinates (-6, -3) and coordinates (6, -7)

Enter your answer in slope-intercept form in the box.

Answer 1

Slope Intercept form of the equation is
`y  = (1)/(3) x - 9`

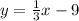
Explanation:

Here, the two point line are given as is A(-6,-3) and B(6,-7)

The slope of the line AB =
`m = (y_2 - y_1)/(x_2 - x_1)`

`m = (-7-(-3))/(6-(-6))   = (-7 + 3)/(6 + 6)   = (4)/(12) \\\implies m = (1)/(3)`

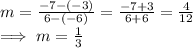
⇒ the slope of AB is m = (4/3)

By SLOPE INTERCEPT FORMULA:

The equation of a line with slope m and a point (x0, y0) is given as

(y-y0)= m (x-x0)

⇒ The equation of line with point (6,-7) is:

`y + 7 = (1)/(3) (x-6)  \implies  3y + 21  - x + 6 - 0\\or, -x + 3y + 27 = 0`

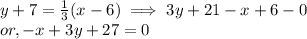
Now, the given equation is -x + 3y = -27

Convert it in the SLOPE INTERCEPT FORM y = mx + c

We get, 3y = x - 27

or,
`y = (1)/(3) x - (27)/(3) \\\implies y = (1)/(3) x - 9`

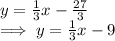
Hence, the Slope Intercept form of the equation is
`y  = (1)/(3) x - 9`