Answer:
Exact solution to the equation is 10-log4(x+6) = 9 is -2
Step-by-step explanation:
As we have given the logarithm equation in the question that
 ……….(1)
……….(1)
Now by using the logarithm property, we know that
x+6>0
So x>-6
Now from equation 1
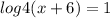
As we know the anti log property as
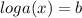 then it becomes
then it becomes
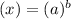
Now by using anti log Properties, the above equation would becomes
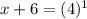
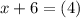
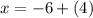
So x=-2
Hence the possible value of x that satisfy the given logarithm equation is -2.