Question

Answer correclty

What is the first step to writing an equation in slope-intercept form using the given points: (-1, 0), (-2, -2).

A) Use point-slope form

B) Substitute -1 for x and 0 for y in y = mx + b

C) Find the slope using the slope formula
y2 - y1
x2 - x1

D) Find the slope using the slope formula y = mx + b

Answer 1

4. C)
`(3, -2)`

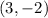
3. B) 9,6 = the number of points you would increase each hour of studying; 65,8 = your score if you studied 0 hours

2. B) The events have a strong positive linear correlation.

1. C) Find the slope using the slope formula:

`(y_2 - y_1)/(x_2 - x_1)`

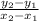
Explanation:

4. (−7, 10) → 10 = 7 + 3 ☑

(−1, 4) → 4 = 1 + 3 ☑

(0, 3) → 3 = 0 + 3 ☑

(3, −2) → −2 ≠ −3 + 3; 0 ☒

3. You obviously have to plug "0" in for x to get your initial value of 65,8, which represents the minimum value of points you would receive if you never were to study, and of course, the 9,6 is the average score increased for every hour studied.

2. The correlation coefficient is 0,02, which is positive, so this would be the obvious choice.

1. You CANNOT write a linear equation without FIRST finding the rate of change [slope]. You will ALWAYS need the rate of change in order to write any linear equation.

I am joyous to assist you anytime.

Answer 2

C) Find the slope using the slope formula.

Explanation:

The first step to find the slope-intercept form is to calculate the slope using its definition

`m=(y_(2)-y_(1) )/(x_(2)-x_(1) )`

Replacing the given points
`(-1,0),(-2,-2)`, we have

`m=(-2-0)/(-2-(-1)) =(-2)/(-2+1) =(-2)/(-1)=2`

So, the slope is 2.

Now, we use the slope-intercept formula

`y-y_(1) =m(x-x_(1) )`

Replacing one point and the slope, we have the slope-intercept form

`y-y_(1) =m(x-x_(1) )\\y-0=2(x-(-1))\\y=2x+1`

Which is a line with slope of 2 and y-intercept at 1.

Therefore, the right answer is C, because the first step to find the slope-intercept form, we have to find the slope first.