Answer:
Option C.
Explanation:
The given function is
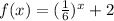
We need to find the domain and range of the function.
Domain is the set of input values.
The given function is an exponential function. This exponential function is defined for all real values of x. So,
Domain : x is a real number
Range is the set of output values.
We know that
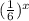 is always greater than 0.
is always greater than 0.
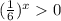
Add 2 on both sides.
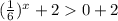
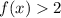
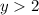
So, the rage of the function is
Range: y
Therefore, the correct option is C.