Answer:
Gravitational potential energy of the satellite: approximately
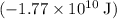 . (Note that this value is negative.)
. (Note that this value is negative.)
Magnitude of the gravitational force between the earth and the satellite: approximately
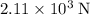
Step-by-step explanation:
(a)
Consider the formula for the gravitational potential energy (GPE) between two dot or spherical mass:
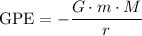 ,
,
where
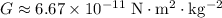 is the gravitational constant,
is the gravitational constant,
 and
and
 are the mass of the two objects, and
are the mass of the two objects, and
 is the separation between the center of mass of the two objects.
is the separation between the center of mass of the two objects.
Note the negative sign in front of the fraction. Electrostatic force might either be attractive or repulsive. However, gravity between two object of mass is always attractive. As a result, unlike electrical potential energy, the gravitational potential energy between two objects with mass should always be negative.
Keep in mind that the center of mass of a sphere with uniform density is at its center. If the earth is approximated as a sphere like that, its center of mass wouldn't be on the surface (i.e. the ground.) Rather, the center of the earth's mass should be somewhere deep underground near its core.
Look up the following quantities:
- Mean radius of the earth (average distance between the core and the surface:) approximately
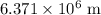 .
. - Mass of the earth: approximately
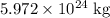 .
.
The distance between the satellite and the center of mass of the earth comes in two parts:
- distance between the satellite and the surface of the earth, and
- distance between the surface of the earth and its center of mass.
In other words,
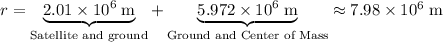 .
.
Make sure that all values are in standard units and apply the formula:
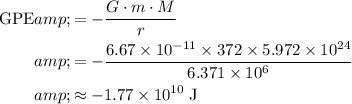 .
.
Since all inputs are in their standard units, the unit of the output (potential energy) should be in joules, which is the standard unit of energy.
(b)
The formula for the magnitude of gravitational force between two points (or sphere) of mass is
 .
.
Note that as a magnitude, the output of this formula should always be positive. Evaluate this formula for the same
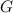 ,
,
 ,
,
 , and
, and
 as in part (a) of this problem:
as in part (a) of this problem:
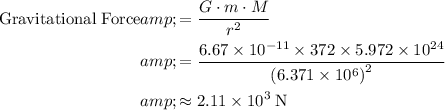 .
.