Question

To drive a typical car at 40 mph on a level road for onehour requires about 3.2 × 107 J ofenergy. Suppose one tried to store this much energy in a spinningsolid cylindrical flywheel which was then coupled to the wheels ofthe car. A large flywheel cannot be spun too fast or it willfracture. If one used a flywheel of radius 0.60 m and mass 400 kg,what angular speed would be required to store 3.2 ×107 J (Incidentally, 2500 rpm is about the maximumfeasible rate of revolution with present materials technology forsuch a flywheel.)

a. 943 rad/s

b. 530 rad/s

c. 1800 rad/s

d. 3620 rad/s

e. 5470 rad/s

Answer 1

`\omega=943\ rad/s`

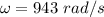
Step-by-step explanation:

Given that,

Speed of the car, v = 40 mph

Energy required,
`E=3.2* 10^7 J`

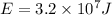
Radius of the flywheel, r = 0.6 m

Mass of flywheel, m = 400 kg

The kinetic energy of the disk is given by :

`E_k=(1)/(2)I\omega^2`

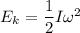
I is the moment of inertia of the disk,
`I=(mr^2)/(2)`

`\omega^2=(2E_k)/(I)`

`\omega^2=(2E_k)/((mr^2)/(2))`

`\omega^2=(2* 3.2* 10^7)/((400* (0.6)^2)/(2))`

`\omega=942.80\ rad/s`

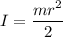
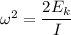
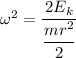
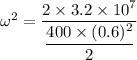
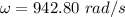
or

`\omega=943\ rad/s`

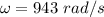
So, the angular speed of the disk is 943 rad/s. Hence, this is the required solution.