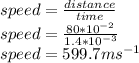Question

A bullet we shot through two cardboard discs, which have a distance of 80 cm from each other. These two cardboard discs rotate on a shaft with a circulation time of 6.67 x 10-4 min. What speed does the bullet have when both bullet points are shifted by 12 ° from each other?

Answer 1

`599.7 ms^(-1)`

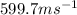
Step-by-step explanation:

Assume that the bullet is shot at a velocity of (v m/s) and it will take t time to pass the second plate.

by the definition of then angular velocity (ω)

ω=\frac{angular displacement}{time }[/tex]

`=(360degrees)/(6.67*10^(-4) *60 )\\=8995.5 deg/s`

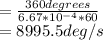
Lets find the time to turn the next plate by 12 degrees , using θ=ωt

]t=\frac{12}{8995.5} =1.334*10^{-3}[/tex]

the bullet has to travel 80cm in this much of time to make a hole in the second plate. We can find the speed using this equation

(we have to convert cm into meters first)

`speed=(distance)/(time)\\speed=(80*10^(-2) )/(1.4*10^(-3) ) \\speed=599.7 ms^(-1)`