Question

The "Garbage Project" at the University of Arizona reports that the amount of paper discarded by households per week is normally distributed with mean 9.4 lb and standard deviation 4.2 lb. What percentage of households throw out at least 8 lb of paper a week? (Round your answer to one decimal place.)

Answer 1

Answer:13.05 %

Explanation:

Given

mean
`\mu =9.4 lb`

standard deviation
`\sigma =4.2 lb`

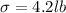
Let X be the amount of paper discarded from households per week normally distributed

we need to find
`P(X> 8)`

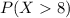
suppose
`z=(X-9.4)/(4.2)`

`P(X>8)=P((X-9.4)/(4.2)>(8-9.4)/(4.2))`

`=P(z> -0.333)`

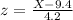
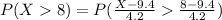
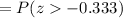
Since standard normal is perfectly symmetric about the mean

therefore
`P(z > -0.33)=P(z < 0.33)`

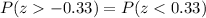
For Normal distribution

`P(a\leq z\leq b)=P\left ( a\leq z\leq b\right )=(1)/(√(2\pi ))\int_(a)^(b)e^{(z^2)/(2)}dz`

`P(z<0.33)=(1)/(√(2\pi ))\int_(0)^(3)e^{(z^2)/(2)}dz`

`P(z<0.33)=(0.1636√(2))/(√(\pi ))`

`P(z<0.33)=0.13054`

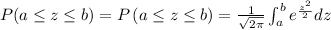
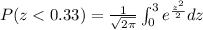
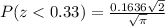
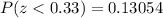
Thus
`P(z> -0.33)=0.13054`

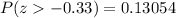
Therefore 13.05 % of households throw out at least 8 lb of paper a week