Question

Help with homework question

Answer 1

The solution set is { 66.6°, 113.4°, 192.6°, 347.4° }.

Explanation:

Given:

The given equation in the interval (0°,360°) is given as:

`10\sin ^(2)\theta - 7\sin \theta=2`

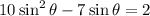
Adding -2 both sides, we get

`10\sin ^(2)\theta - 7\sin \theta-2=2-2\\10\sin ^(2)\theta - 7\sin \theta-2=0`

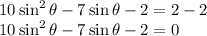
This is a quadratic equation in
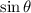`\sin \theta` of the form
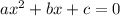`ax^2+bx+c=0`. Solve it using the quadratic formula given as:

`\sin \theta=\frac{-b\pm \sqrt{b^(2)-4ac}}{2a}`

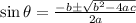
Here,
`a=10,b=-7,c=-2`

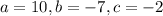
Therefore,

`\sin \theta=\frac{-(-7)\pm \sqrt{(-7)^(2)-4(10)(-2)}}{2(-2)}\\\sin \theta=0.918\textrm{ or }\sin \theta = -0.218`

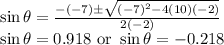
Now, taking inverse of the sine values, we get

`\theta=\sin^(-1)(0.918)\textrm{ or }\theta=\sin^(-1)(-0.218)\\\theta=66.6\textrm{ or }\theta=-12.59`

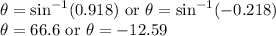
But, we need to find
`\theta` in the interval (0°,360°).

`\textrm{For interval (0,180)}\\\sin\theta=sin(180-\theta)\\\\\textrm{For interval (180,270)}\\\sin\theta=sin(180+\theta)\\\\\textrm{For interval (180,360)}\\\sin\theta=sin(360-\theta)`

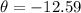`\theta=-12.59` is in the fourth quadrant, So, its positive value is:

`360-12.59=347.41`°

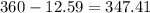Also, from unit circle, sine of the angle in third and fourth quadrants are same. So,

`12.59=180+12.59=192.59`°

`66.6=180-66.6=113.4`°

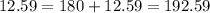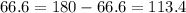Therefore, the set of angles for which the above equation is satisfied in the interval (0°,360°) is { 66.6°, 113.4°, 192.6°, 347.4° }.