Question

Suppose lines EF and GH are reflected over the line Y equals X to form the lines JK and LM which statement would be true about the lines

A) jk and lm will be parallel

B) jk and lm will be perpendicular

C) jk will be same slope as ef

D) lm will be negative reciprocal of gh

Answer 1

A) JK and LM will be parallel to each other.

Explanation:

On reflection on
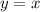`y=x` line the x co-ordinate changes with y co-ordinate and y co-ordinate changes with x co-ordinate

`(x,y)\rightarrow (y,x)`

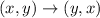
Points on line EF

`(0,6) , (-5,-2)`

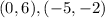
On reflection of this line on
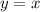`y=x` the new points we get for line JK are

`(6,0),(-2,-5)`

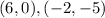
Points on line GH

`(-4,9),(-9,1)`

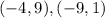
On reflection on y=x line the new points we get for line LM are

`(9,-4),(1,-9)`

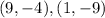
Slope of line JK

`m=(y_2-y_1)/(x2-x1)\\m=((-5)-0)/((-2)-6) \\m=(-5)/(-8)=(5)/(8)`

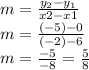
Slope of line LM

`m=(y_2-y_1)/(x2-x1)\\m=((-9)-(-4))/(1-9) \\m=(-9+4)/(-8)=(-5)/(-8)\\m=(5)/(8)`

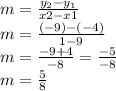
For two line to be parallel, their slopes will be same.

`m_(JK) =(5)/(8) , m_(LM)=(5)/(8)`

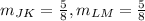
Since slopes of lines JK and LM are same therefore we can say that these are parallel to each other.