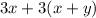Question

Which expressions are equivalent to 3x+3(x+y)3x+3(x+y)3, x, plus, 3, left parenthesis, x, plus, y, right parenthesis ? Choose all answers that apply: Choose all answers that apply: (Choice A) A 6x+3y6x+3y6, x, plus, 3, y (Choice B) B 3(x+x+y)3(x+x+y)3, left parenthesis, x, plus, x, plus, y, right parenthesis (Choice C) C 3xy3xy

Answer 1

Answer: Choise A and Choise B.

Explanation:

Given the following expression:

`3x+3(x+y)`

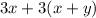
You can simplify it in order to find equivalent expressions.

Appying the Distributive Property, you get:

`3x+(3)(x)+(y)(3)=3x+3x+3y`

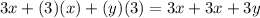
So:

1. If you add the like terms, you get this equivalent expression:

`3x+3x+3y=6x+3y`

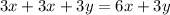
2. But if you factor out 3, you get the following equivalent expression:

`3x+3x+3y=3(x+x+y)`

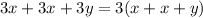
Therefore, the expression shown in Choice A and Choise B are equivalents to the expression
`3x+3(x+y)`