Question

Mars has a mass 1/10 that of earth and a diameter 1/2 that of earth

Answer 1

Answer: D.
`4 m/s^(2)`

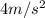
Step-by-step explanation:

The question is incomplete, please remember to write the whole question. However, the the complete question is as follows:

Mars has a mass 1/10 that of Earth and a diameter 1/2 that of Earth. The acceleration of a falling body body near the surface of Mars is most nearly:

A.
`0.25 m/s^(2)`

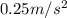
B.
`0.5 m/s^(2)`

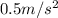
C.
`2 m/s^(2)`

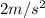
D.
`4 m/s^(2)`

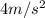
E.
`25 m/s^(2)`

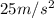
Let's begin by the fact that on Earth, the gravity force
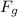`F_(g)` that acts on a falling object is given by:

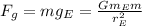`F_(g)=mg_(E)=(Gm_(E)m)/(r_(E)^(2))` (1)

Where:

`m` is the mass of the falling body

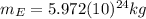`m_(E)=5.972(10)^(24) kg` is the mass of the Earth

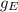`g_(E)` is the acceleration due gravity on Earth

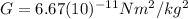`G=6.67(10)^(-11) Nm^(2)/kg^(2)` is the Universal Gravitational constant

`r_(E)=(d_(E))/(2)=6371000m` is the Earth's radius and
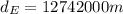`d_(E)=12742000 m` is its diameter

Simplifying (1) we have:

`g_(E)=(Gm_(E))/(r_(E)^(2))` (2)

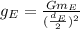`g_(E)=(G m_(E))/(((d_(E))/(2))^(2))` (3)

Now, in the case of Mars we have:

`g_(M)=(G m_(M))/(((d_(M))/(2))^(2))` (4)

Where:

`m_(M)=(1)/(10)m_(E)`

`d_(M)=(1)/(2)d_(E)`

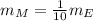
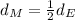
Substituting these on (4):

`g_(M)=(G (1)/(10)m_(E))/((((1)/(2)d_(E))/(2))^(2))` (5)

Simplifying:

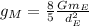`g_(M)=(8)/(5) (G m_(E))/(d_(E)^(2))` (6)

Then:

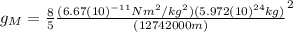`g_(M)=(8)/(5) ((6.67(10)^(-11) Nm^(2)/kg^(2))(5.972(10)^(24) kg))/((12742000 m))^(2)}` (7)

Finally:

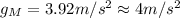`g_(M)=3.92 m/s^(2) \approx 4 m/s^(2)` This is most nearly the acceleration of a falling body near the surface of Mars