Answer:
Option 1 - Down on the left down on the right
Explanation:
Given : Function
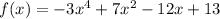
To find : Without using technology, describe the end behavior of f(x) ?
Solution :
Without technology we apply characteristics of Power and Polynomial Functions
As in function
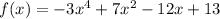
The the end behavior of power functions of the form
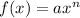 where n is a non-negative integer depending on the power and the constant.
where n is a non-negative integer depending on the power and the constant.
The leading term,
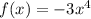
Negative constant and even power.
So, At
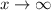
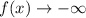
At
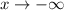
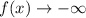
i.e. the curve approaches down on the left and down on the right.
Therefore, option 1 is correct.