Question

Given your intended theoretical yield of 15.0 g of alum, KAl(SO4)2.12 H2O, calculate the amount of aluminum required for the " reduced-scale" synthesis. Use this result (along with the 12.0 g Al suggested in the original procedure) to calculate the value of the scaling factor by which all reagents must be reduced.

Answer 1

Answer : The value of the scaling factor by which all reagents reduced must be 0.0711

Explanation :

First we have to calculate the molecular weight of alum.

The formula of alum is,
`KAl(SO_4)_2.12H_2O`

Molecular weight of Alum =
`39+27+2* (32+16* 4)+12* (2*1+16)=474g/mol`

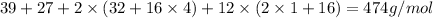
Now we have to calculate the moles of alum.

`\text{Moles of }PbS=\frac{\text{Mass of }PbS}{\text{Molar mass of }PbS}=(15.0g)/(474g/mole)=0.0316mole`

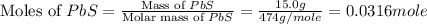
Now we have to calculate the moles of aluminium.

From the molecular formula of the alum we conclude that, 1 mole of alum constitutes 1 mole of aluminium.

So, 0.0316 moles of alum constitutes the number of moles of aluminium = 0.0316 moles

Now we have to calculate the mass of aluminum.

Molar mass of aluminium = 27 g/mole

`\text{ Mass of }Al=\text{ Moles of }Al* \text{ Molar mass of }Al`

`\text{ Mass of }Al=(0.0316moles)* (27g/mole)=0.853g`

Now we have to calculate the value of the scaling factor.

In the the original procedure, the amount of aluminium required = 12.0 g

The amount of aluminium required to produce 15 gram alum = 0.853 g

The scaling factor =
`(0.853)/(12)=0.0711`

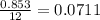
Therefore, the value of the scaling factor by which all reagents reduced must be 0.0711