Question

Which of the following sets of lengths can Sean use to make a right triangle?

Group of answer choices

{5 cm, 15 cm, 18 cm}

{6 cm, 12 cm, 16 cm}

{5 cm, 13 cm, 15 cm}

{8 cm, 15 cm, 17 cm}

Answer 1

{8 cm, 15 cm, 17 cm}

Explanation:

we know that

The length sides of a right triangle must satisfy the Pythagoras Theorem

so

`c^2=a^2+b^2`

where

c is the greater side (the hypotenuse)

a and b are the legs (perpendicular sides)

Verify each case

case 1) we have

{5 cm, 15 cm, 18 cm}

substitute in the formula

`18^2=5^2+15^2`

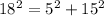
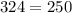`324=250` ----> is not true

therefore

Sean cannot make a right triangle with this set of lengths

case 2) we have

{6 cm, 12 cm, 16 cm}

substitute in the formula

`16^2=8^2+12^2`

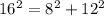
`256=208` ----> is not true

therefore

Sean cannot make a right triangle with this set of lengths

case 3) we have

{5 cm, 13 cm, 15 cm}

substitute in the formula

`15^2=5^2+13^2`

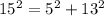
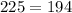`225=194` ----> is not true

therefore

Sean cannot make a right triangle with this set of lengths

case 4) we have

{8 cm, 15 cm, 17 cm}

substitute in the formula

`17^2=8^2+15^2`

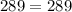`289=289` ----> is true

therefore

Sean can make a right triangle with this set of lengths