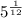Question

Please make sure that it's the correct answer!

Simplify cube root of 5 over fourth root of 5.

A. 5 to the power of one fourth
B. 5 to the power of one twelfth
C. 5 to the power of seven twelfths
D. 5 to the power of four thirds

Answer 1

`5^{(1)/(12)}`

Explanation:

The given expression is:

`\frac{\sqrt[3]{5} }{\sqrt[4]{5} }`

To simplify this expression we need to apply the exponent property that allows to transform from radical expression to a power with a fraction exponent, the property states:

`\sqrt[n]{x^(m) }=x^{(m)/(n) }`

Applying the property we have:

`\frac{\sqrt[3]{5} }{\sqrt[4]{5} }\\\frac{(5)^{(1)/(3) } }{(5)^{(1)/(4) } } \\5^{(1)/(3)-(1)/(4)}=5^{(4-3)/(12)}=5^{(1)/(12)}`

Therefore, the simplified expression is
`5^{(1)/(12)}`

Answer 2

B

Explanation:

In the attached file