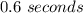Answer:
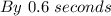
Explanation:
The missing equations are:
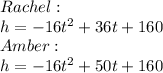
Make each equation equal to 0 and then apply the the Quadratic formula
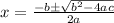
Time it takes Rachel's textbook to reach the ground (in seconds)
Having the equation:
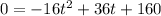
We can identify that:
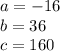
Substituting values into the Quadratic formula, we get:
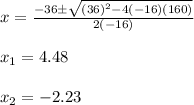
Time it takes Amber's textbook to reach the ground (in seconds)
Having the equation:
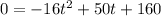
We can identify that:
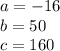
Substituting values into the Quadratic formula, we get:
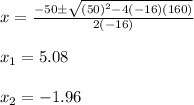
The difference of the positive values is:
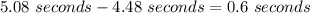
Therefore, Rachel's textbook beat Amber's to the ground by