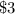Answer:
Price of each senior citizen ticket is
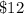 and one child ticket is
and one child ticket is
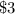
Explanation:
Let the price of each senior citizen ticket be x.
Let the price of each Child ticket be y.
Tickets sold on first day which are given as,
5 senior citizen tickets and 14 child tickets for a total of $102.
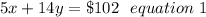
Tickets sold on first day which are given as,
$153 on the second day by selling 11 senior citizen tickets and 7 child tickets.
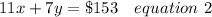
Now multiplying by 2 equation 2 we get
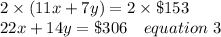
Now Subtracting equation 1 from equation 3 we get
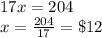
Substituting value of x in equation 1 we get
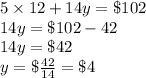
Hence Senior Citizen ticket price is
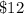 and Child ticket price is
and Child ticket price is