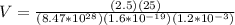Question

The cross section of a copper strip is 1.2 mmthick and 20 mm wide. There is a 25-A current through this cross section, with the charge carriers traveling down the length of the strip. The strip is placed in a uniform magnetic field that has a magnitude of 2.5 T and is directed perpendicular to both the length and the width of the strip. The number density of free electrons in copperis 8.47 ×1019mm−3. a. Calculate the speed of the electrons in the strip. b. Calculate the potential difference across the strip width.

Answer 1

To solve this problem it is necessary to use the concepts related to the Hall Effect and Drift velocity, that is, at the speed that an electron reaches due to a magnetic field.

The drift velocity is given by the equation:

`V_d = (I)/(nAq)`

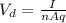
Where

I = current

n = Number of free electrons

A = Cross-Section Area

q = charge of proton

Our values are given by,

`I = 25 A`

`A= 1.2*20 *10^(-6) m^2`

`q= 1.6*10^(-19)C`

`N = 8.47*10^(19) mm^(-3)`

`V_d =(25)/((1.2*20 *10^(-6))(1.6*10^(-19))(8.47*10^(19) ))`

`V_d = 7.68*10^(-5)m/s`

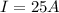
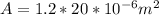
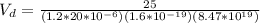
The hall voltage is given by

`V=(IB)/(ned)`

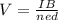
Where

B= Magnetic field

n = number of free electrons

d = distance

e = charge of electron

Then using the formula and replacing,

`V=((2.5)(25))/((8.47*10^(28))(1.6*10^(-19))(1.2*10^(-3)))`

`V = 3.84*10^(-6)V`