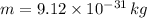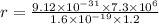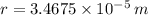Answer:
a)
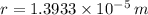
b)
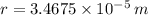
Step-by-step explanation:
(a)
Given that:
magnetic field,
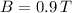
velocity of an electron,
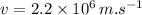
we know the charge on an electron,
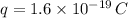
Since the direction of velocity and magnetic field are not mentioned therefore we assume it to be mutually perpendicular to each other so that it makes a circular trajectory.
For such a case, we have the formula of radius as:
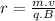
where m= mass of the charge.
here
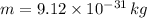

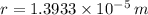
(b)
magnetic field,
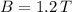
velocity of an electron,
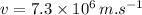
we know the charge on an electron,
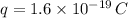
Since the direction of velocity and magnetic field are not mentioned therefore we assume it to be mutually perpendicular to each other so that it makes a circular trajectory.
For such a case, we have the formula of radius as:
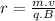
where m= mass of the charge.
here