Answer:
C) The value of r = 50 units.
Explanation:
Measure of Circle 1 are (C, d, and r)
and Measure of Circle 2 are (C', d', and r')
Also, C /C' = 5 and d' = 20
CIRCUMFERENCE OF A CIRCLE = 2 π x RADIUS
= π x DIAMETER (as D = 2 x Radius)
Circumference of Circle 1 : C = π x d
Circumference of Circle 2 : C' = π x d'
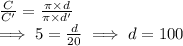
⇒ d = 100
As D = 2 x Radius .⇒ r = d/2 = 100/2 = 50
or, r = 50
Hence, the value of r = 50 units.