Question

In parallelogram ABCD , m∠A=(2x)° and m∠B=(5x+5)° . The figure shows parallelogram A B C D with vertices named clockwise from bottom left. What are the measures of the angles of the parallelogram? Enter your answers in the boxes. m∠A= ° m∠B= ​ ° m∠C= ° m∠D= °

Answer 1

The measure of angles of parallelogram are

∠A = 50° ,

∠B = 130° ,

∠C = 50° ,

∠D = 130°

Explanation:

Given as for a parallelogram :

The vertices of parallelogram is A B C D in clockwise

The measure of angle A = ∠A = ( 2 x )°

The measure of angle B = ∠B = ( 5 x + 5 )°

Now, for a parallelogram , the sum of measure of all four angles = 360°

From The property of Parallelogram

A ) The adjacent angles are supplementary

So, ∠A + ∠B = 180°

Or, ( 2 x )° + ( 5 x + 5 )° = 180°

Or, ( 7 x + 5 )° = 180°

Or , ( 7 x )° = 180° - 5°

Or , ( 7 x )° = 175°

∴ x =
`(175)/(7)`

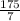
I.e x = 25°

So, ∠A = ( 2 x )° = ( 2 ×25° )

I.e , ∠A = 50°

∠B = ( 5 x + 5 )°

Or, ∠B = ( 5 ×25° + 5 )°

I.e , ∠B = 130°

B ) The opposite angles of parallelogram is equal

So, ∠C = ∠A = 50°

I,e ∠C = 50°

And ∠D = ∠B = 130°

I.e ∠D = 130°

Hence The measure of angles of parallelogram are ∠A = 50° , ∠B = 130° , ∠C = 50° , ∠D = 130° Answer