Answer:
According to the theorem,
if
 , then
, then
 .
.
If
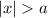 , then
, then
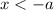 or
or
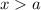
So, in this case, we have to apply the second case.

Then, we have the following compound inequiality

These inequalities represent the solution for the problem. If we solve both of them, we have
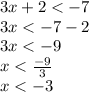
And,
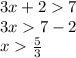
This means that the solution for the given inequality comprehend all number less than -3 and more than 5/3.