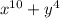Question

Factor x^10 +y^4 using the sum of squares
(hint: x^10 = (x^5)^2 and y^4 = (y^2)^2)

Answer 1

`x^(10) +y^4` cannot be factorized that is cannot be represented as products of lower degree polynomials.

Solution:

Need to factor
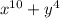`x^(10) +y^4` using the sum of squares that is we need to factorize
`x^(10) +y^4`

`x^(10)+y^(4)=x^((5 * 2))+y^((2 * 2))`

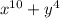
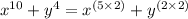
Using law of exponent
`\mathrm{a}^{(\mathrm{m} * \mathrm{n})}=\left(\mathrm{a}^{\mathrm{m}}\right)^{\mathrm{n}}`

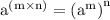
On applying this we get,

`x^(10)+y^(4)=\left(x^(5)\right)^(2)+\left(y^(2)\right)^(2)`

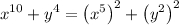
But there is no direct formula of
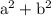`\mathrm{a}^(2)+\mathrm{b}^(2)` which can provide factors.

Hence we can say that
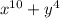`x^(10) +y^4` cannot be factorize that is cannot be represented as products of lower degree polynomials.