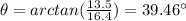Question

A firecracker breaks up into several pieces, one of which has a mass of 200 g and flies off along the x-axis with a speed of 82.0 m/s. A second piece has a mass of 300 g and flies off along the y-axis with a speed of 45.0 m/s. What are the magnitude and direction of the total momentum of these two pieces?

Answer 1

`p=21.24\ kg\ m/s`

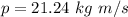
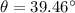`\theta=39.46^(\circ)` over the x axis.

Step-by-step explanation:

We have to add their linear momentum as a vector.

For piece 1:

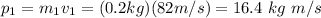`p_1=m_1v_1=(0.2kg)(82m/s)=16.4\ kg\ m/s` along the x axis.

For piece 2:

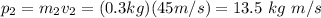`p_2=m_2v_2=(0.3kg)(45m/s)=13.5\ kg\ m/s` along the y axis.

Since both are perpendicular, we get the the magnitude of the vectorial sum of them with:

`p=√(p_1^2+p_2^2)=√((16.4\ kg\ m/s)^2+(13.5\ kg\ m/s)^2)=21.24\ kg\ m/s`

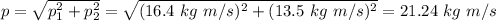
And the angle over the x axis can be calculated as:

`\theta=arctan((13.5)/(16.4))=39.46^(\circ)`