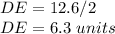Answer:

Explanation:
see the attached figure to better understand the problem
we know that
If two figures are similar, then the ratio of its corresponding sides is proportional and its corresponding angles are congruent
In this problem
Triangles ABC and DBE are similar by AA Similarity Theorem
so
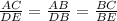
we have
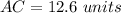

substitute
![(12.6)/(DE)=(2DB)/(DB)/tex]</p><p>Simplify</p><p>[tex](12.6)/(DE)=2](https://img.qammunity.org/2020/formulas/mathematics/middle-school/tiaxcvyvteafbo0dodmvyrxh8ssyu2ugxt.png)